
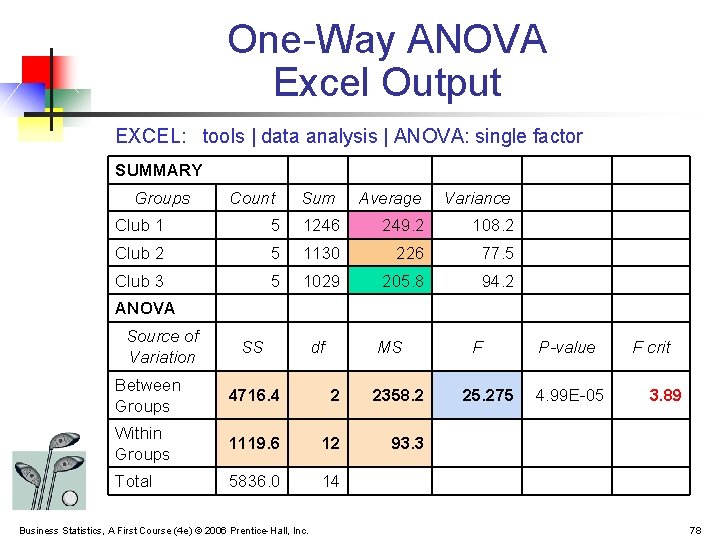
Note that this data range can be obtained from the data in Figure 1 by inserting the array formula =RESHAPE(G5:I14) in range K2:M32 and pressing Ctrl-Shft-Enter.Īs can be seen from cell T13, the one-factor test shows there is a significant difference between the three types of training programs, which as we have seen is an incorrect result.
Only the first 15 rows of the data are shown on the left side of Figure 4. If we ignore the Offices and simply perform a one-way ANOVA, we obtain the results shown in Figure 4. We see from the nested analysis that the Training effect (Factor A) is not significant (cell R17), unlike the result obtained from the two fixed factor analysis (cell R7). We are not particularly interested in the Col (Rows) effect, but we are interested in the Training effect (labelled Rows). The following changes are made: cell M18 contains the formula =M8+M9, cell N18 contains the formula =N8+N9 and cell P17 contains the formula =O17/O18 (instead of =O17/O19). We now modify this analysis to obtain the nested analysis shown on the bottom right side (range L13:R20) of Figure 3. The output is shown on the upper right side (range 元:R11) of Figure 3. We next use the Real Statistics Anova: two-factor data analysis tool on the data in range A3:D33. The complete data is contained in the range A3:D33. Note that all the Conflict Management and Psychology data elements are shown in Figure 3, but only the first two (of ten) rows of the Negotiation data elements are shown due to a lack of space. The first thing we need to do is to stack the input data from Figure 1 in the form shown on the left side of Figure 3.
Anova data analysis excel how to#
We will then show how to perform the analysis using the Real Statistics Nested ANOVA data analysis tool. Just as we did in Two-Factor Mixed ANOVA, we first show how to perform the analysis using a modified version of either Excel’s Two Factor ANOVA with Replication data analysis tool or Real Statistics’ Anova: two-factor data analysis tool as shown in Figure 3. The design for that model is shown in Figure 2 below (as well as in Figure 1 of Two Factor Mixed ANOVA, which shows there are interactions between the Office and Testing factors). Note the difference between this model and the two factor mixed design described in Example 1 of Two Factor Mixed ANOVA. In fact, as Figure 1 captures, we have a nested model whereby the field office factor is nested under the training program factor. We can’t perform a two-way ANOVA since each field office has only one training program and so there are no intersection data elements. The problem with this approach is that perhaps the field office has some impact on the result and can’t simply be ignored. We could therefore conduct a one-factor ANOVA, ignoring the field office information. In this example, training program is a fixed factor and field office is a random factor.įor this example, we are only interested in the training program factor and not the field office factor. It then selected 10 FBI agents at random from each of the nine offices and gave each of the 90 agents a test to assess their skills.
The research group decides to randomly select three field offices that have only conducted Conflict Management training, three field offices that have only conducted Psychology training and three field offices that have only conducted Negotiation training. Throughout the country, local FBI field offices have conducted one or more of these types of training. Example 1: A research group wants to study the effectiveness of three types of training programs (Conflict Management, Psychology and Negotiation) for FBI agents’ preparedness for dealing with local youth who may become involved in terrorist attacks.


 0 kommentar(er)
0 kommentar(er)
